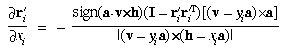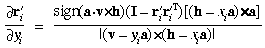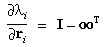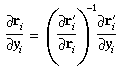Least-Squares Camera Calibration Including Lens Distortion and
Automatic Editing of Calibration Points
Donald B. Gennery
Jet Propulsion Laboratory
California Institute of Technology
Abstract
A method is described for calibrating cameras including radial lens
distortion, by using known points such as those measured from a
calibration fixture. The distortion terms are relative to the optical
axis, which is included in the model so that it does not have to be
orthogonal to the image sensor plane. A priori standard deviations
can be used to apply weight to zero values for the distortion terms
and to zero difference between the optical axis and the perpendicular
to the sensor plane, so that the solution for these is well determined
when there is insufficient information in the calibration data. The
initial approximations needed for the nonlinear least-squares
adjustment are obtained in a simple manner from the calibration data
and other known information. Outliers among the calibration points
are removed by means of automatic editing based on analysis of the
residuals. The use of the camera model also is described, including
partial derivatives for propagating both from object space to image
space and vice versa.
1 Introduction
The basic camera model that we have been using in the JPL robotics
laboratory was originally developed here by Yakimovsky and Cunningham
[YAKIMOVSKY&CUNNI1978].
It included a central (perspective) projection and an arbitrary affine
transformation in the image plane, but it did not include lens
distortion. In 1986, the present author developed a better method of
calibrating that model, by using a rigorous least-squares adjustment
[5]. In 1990, that camera model and the method for its calibration
were extended to include radial lens distortion [GENNERY1991]. An improved version was
described in a workshop in 1992 [GENNERY1992]. This paper describes the
improved model, the adjustment algorithm, and the mathematics for the
use of the camera model, including subsequent refinements. However,
the method of measuring the calibration data (finding the dots in
images of a calibration fixture [GENNERYETAL1987]) has not changed,
and thus its description will not be repeated here.
The camera model used here should be adequate for producing accurate
geometric data, except in the following three situations. First, a
fish-eye lens has a very large distortion for which the distortion
polynomial used here would not converge. (In fact, the distortion as
defined here can be infinite, since the field of view can exceed
180°.) For such a lens the image coordinate should be represented
as being ideally proportional to the off-axis angle, instead of the
tangent of this angle as in the perspective projection. Then, a small
distortion could be added on top of this. Furthermore, the position
of the entrance pupil of a fish-eye lens varies greatly with the
off-axis angle to the object; therefore, this variation would have to
be modeled unless all viewed objects are very far away. Second, even
for an ordinary lens, the entrance pupil moves slightly, so that if
objects very close to the lens are viewed, the variation again would
have to be included in the camera model. Third, if there is
appreciable nonradial distortion, such as might be produced by
distortion in the image sensor itself or by a lens with badly
misaligned elements, it would require a more elaborate model than the
radial distortion used here. However, this situation should not occur
with a CCD camera with a well-made lens, unless an anamorphic lens is
used. (A small amount of decentering in the lens and a CCD
synchronization error that is a linear function of the position in the
image are subsumed by terms included in the camera model.)
The calibration method presented here applies at only one lens
setting. For a zoom lens, a separate calibration would have to be
done at each zoom setting. Similarly, if focus is changed, a separate
calibration is needed at each focus setting.
In this paper, for physical vectors in three-dimensional space, the
dot product will be indicated by · and the cross product by
×. For any such vector v, its length ( ) will be represented by
|v|, and the unit vector in its direction
(v/|v|) will be represented by
unit(v). The derivative of a vector relative to a
scalar will be considered to be a vector, the derivative of a scalar
relative to a vector will be considered to be a row vector, and the
derivative of a vector relative to a vector will be considered to be a
matrix.
) will be represented by
|v|, and the unit vector in its direction
(v/|v|) will be represented by
unit(v). The derivative of a vector relative to a
scalar will be considered to be a vector, the derivative of a scalar
relative to a vector will be considered to be a row vector, and the
derivative of a vector relative to a vector will be considered to be a
matrix.
2 Definition of Camera Model
2.1 Camera Model without Distortion
The old camera model [YAKIMOVSKY&CUNNI1978]
(without distortion) consisted of the four 3-vectors
c, a, h, and
v, expressed in object (world) coordinates, which
have the following meanings. The entrance pupil point of the camera
lens is at position c. Let a perpendicular be
dropped from the exit pupil point to the image sensor plane, and let
its point of intersection with this plane be denoted by
xc and yc in image
coordinates. (Decentering in the lens causes the actual values of
xc and yc to differ from those
according this definition.) Then a is a unit vector
parallel to this perpendicular and pointing outwards from the camera
to the scene. Furthermore, let v' and
h' be vectors in the sensor plane and perpendicular
to the x and y image axes, respectively (usually
considered to be horizontal and vertical, respectively, but not
necessarily orthogonal) of the image coordinate system, with each
magnitude equal to the change in the image coordinate (usually
measured in pixels) caused by a change of unity in the tangent of the
angle from the a vector to the viewed point,
subtended at the entrance pupil point. (If the entrance and exit
pupil points coincide with the first and second nodal points, as is
approximately the case for typical cameras with other than zoom or
telephoto lenses, this is equivalent to saying that the magnitude of
h' or v' is equal to the distance
from the second nodal point to the sensor plane, expressed in
horizontal pixels or vertical pixels, respectively.) Then
h = h' +
xca and
v = v' +
yca. Although these definitions
may seem rather peculiar, they result in convenient expressions for
the image coordinates in terms of the position p of a
point in three-dimensional object space, as follows:
The above equations are given here merely to show the mathematical
relationship represented by the camera model excluding distortion. In
the equations used below for actual data, the subscript I will be used
on quantities associated with individual measured points.
The position c used above often is referred to as the
perspective center. Sometimes, this is assumed to be the first nodal
point of the lens (the same as the first principal point if the medium
is the same on both sides of the lens). However, the rays from the
object (extended as straight lines) must pass through the entrance
pupil if they are to reach the image, so the center of the entrance
pupil is the position from which the camera seems to view the world.
Similarly, the rays to the image seem to emanate from the exit pupil.
If all viewed objects are at the same distance and the camera is
perfectly focused, there is no detectable difference between using
nodal points instead of pupil points in the above definitions, but in
general the distinction should be made; and, if all calibration points
are at the same distance, the calibration cannot determine
c anyway. Of course, mathematically the camera model
is defined by the equations, so the physical meaning of the parameters
does not matter for calibration purposes, as long as they are able to
capture the degrees of freedom in the physical situation, and as long
as the same equations are used in the camera model adjustment and in
the use of the camera model. (For definitions of the terms used here,
see any optics textbook, for example Jenkins and White [JENKINS&WHITE1950]).
2.2 Inclusion of Distortion
Because of symmetry, the displacement due to radial distortion is a
polynomial (in the distance from the optical axis) containing only
odd-order terms. The first-order term is subsumed by the scale
factors included in h and v, if
a is along the optical axis of the lens or if the
pupil points coincided with the respective nodal points, but it must
be included in the general case.
The distortion polynomial must be defined relative to the optical axis
of the lens, in order for the distortion to be radial. If the image
sensor plane is perpendicular to the optical axis, this is the
a vector. However, to allow for the possibility that
they are not exactly perpendicular, a separate unit vector
o is used here for the optical axis. Note that if
there is no distortion and the pupil points coincide with the nodal
points, it is impossible for the calibration to determine the optical
axis. (A central projection is equivalent to using a pinhole camera,
and a pinhole has no axis.) Therefore, some a pnriori weight will be
applied here to tend to make the o vector equal to
the a vector, so that it will be well determined when
there is not much distortion. However, when there is a large
distortion, the data will outweigh this a priori information, and the
two vectors can differ.
Let pi be the three-dimensional
position of any point being viewed. Then the component parallel to
the optical axis of the distance to the point is
The vector to the point orthogonally from the optical axis is
The square of the tangent of the angle from the optical axis to the
point (subtended at the entrance pupil point) is
We can define a proportionality coefficient
µi, that produces the amount of
distortion when multiplied by the off-axis distance to the point, as a
polynomial containing only even-order terms (since we have factored
out the first power). Since  i is proportional to the
square of this off-axis distance, this polynomial can be written as
follows:
i is proportional to the
square of this off-axis distance, this polynomial can be written as
follows:
where the  's are the distortion
coefficients. We use only coefficients up to
's are the distortion
coefficients. We use only coefficients up to  2, since higher-order terms are
negligible except for wide-angle lenses. (In fact, often
2, since higher-order terms are
negligible except for wide-angle lenses. (In fact, often  2 is negligible.) Some a priori
weight (usually a small amount) will be applied to tend to make the
2 is negligible.) Some a priori
weight (usually a small amount) will be applied to tend to make the
 's equal to zero, so that they will be
well determined when there is not enough information in the
calibration images. (This is especially important for high-order
coefficients when there are not many calibration points, and for
's equal to zero, so that they will be
well determined when there is not enough information in the
calibration images. (This is especially important for high-order
coefficients when there are not many calibration points, and for  0 if o and
a are nearly equal or if the pupil points nearly
coincide with the nodal points.) Note that
0 if o and
a are nearly equal or if the pupil points nearly
coincide with the nodal points.) Note that  0 does not actually represent
radial distortion in the usual sense, but is merely a scale factor in
the plane orthogonal to o, whereas the scale factors
included in h and v are in a plane
orthogonal to a.
0 does not actually represent
radial distortion in the usual sense, but is merely a scale factor in
the plane orthogonal to o, whereas the scale factors
included in h and v are in a plane
orthogonal to a.
The effect of distortion can now be written as follows:
where pi is the true position of
the point and p'i is its apparent
position because of distortion.
Then the distorted point can be projected into image coordinates
(denoted by 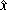 i and
i and
 i) by using
p'i instead of p
in (1, 2). However, for efficiency these equations are expressed in
terms of the intermediate quantities
i) by using
p'i instead of p
in (1, 2). However, for efficiency these equations are expressed in
terms of the intermediate quantities  i,
i, 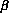 i, and
i, and 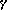 i, as follows, since
these quantities will be needed again in later sections:
i, as follows, since
these quantities will be needed again in later sections:
(The reason for using the circumflex over x and y is
to represent computed values, to distinguish them from measured values
that will be used in Section 4.)
Therefore, the complete camera model consists of the five vectors
c, a, h,
v, and o, where a
and o are unit vectors, and the distortion
coefficients  0,
0,  1, and
1, and  2. This is 18 parameters in all,
of which two are redundant because of the unit vectors. (The
computations can be extended in a straightforward way to include
higher-order
2. This is 18 parameters in all,
of which two are redundant because of the unit vectors. (The
computations can be extended in a straightforward way to include
higher-order  's, if they are ever
needed.)
's, if they are ever
needed.)
3 Partial Derivatives
Partial derivatives of several quantities defined in Section 2 will be
needed in doing the least-squares adjustment of the camera model and
in propagating error estimates when using the camera model. These are
as follows:
where  is the 3-by-3 identity matrix.
The first three of these (derivatives of
is the 3-by-3 identity matrix.
The first three of these (derivatives of 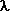 i and
µi) are only intermediate
quantities needed in obtaining the others and will not be used
elsewhere.
i and
µi) are only intermediate
quantities needed in obtaining the others and will not be used
elsewhere.
4 Adjustment of Camera Model
4.1 Data for Adjustment
The calibration data consists of a set of points, with for each point
i its three-dimensional position
pi in object coordinates and its
measured two-dimensional position xi and
yi in image coordinates. Given
information consists of the following: the a priori standard deviation
 d (in radians) of the
difference between the optical axis o and the
a vector, the a priori standard deviations about zero
of each distortion coefficient
d (in radians) of the
difference between the optical axis o and the
a vector, the a priori standard deviations about zero
of each distortion coefficient  0,
0,  1, and
1, and  2 (dimension-less quantities that
in effect are proportionality constants when at an angle of 45°
from the optical axis), the minimum standard deviation of measured
image-coordinate positions
2 (dimension-less quantities that
in effect are proportionality constants when at an angle of 45°
from the optical axis), the minimum standard deviation of measured
image-coordinate positions  m, the nominal focal length of
the camera f, the nominal horizontal and vertical pixel
spacings ph and pv (in the
same units as f), the number of columns
sh and rows sv of pixels in
the camera, and the approximate position of the camera
co in object coordinates. (Reasonable
values for the standard deviations are
m, the nominal focal length of
the camera f, the nominal horizontal and vertical pixel
spacings ph and pv (in the
same units as f), the number of columns
sh and rows sv of pixels in
the camera, and the approximate position of the camera
co in object coordinates. (Reasonable
values for the standard deviations are  d = 0.01,
d = 0.01,  0 = 1 for zoom and telephoto
lenses or 0.1 for ordinary lenses,
0 = 1 for zoom and telephoto
lenses or 0.1 for ordinary lenses,  1 = 1, and
1 = 1, and  2 = 1. On the other hand, any of
the
2 = 1. On the other hand, any of
the  's could be forced to be zero, if
desired, by making their standard deviations very small, perhaps
10-5. The quantities f, ph,
pv, sh,
sv, and c0 are used
primarily in obtaining an initial approximation for iterating, and
thus their exact values are not important.) The desired result
consists of the camera model parameters defined in Section 2, which
where convenient will be assembled into the 18-vector
g = [cT
aT hT
vT oT
's could be forced to be zero, if
desired, by making their standard deviations very small, perhaps
10-5. The quantities f, ph,
pv, sh,
sv, and c0 are used
primarily in obtaining an initial approximation for iterating, and
thus their exact values are not important.) The desired result
consists of the camera model parameters defined in Section 2, which
where convenient will be assembled into the 18-vector
g = [cT
aT hT
vT oT  0
0  1
1  2]T, and their
18-by-18 covariance matrix Cgg, which
indicates the accuracy of the result.
2]T, and their
18-by-18 covariance matrix Cgg, which
indicates the accuracy of the result.
In order to obtain a solution, the input points must not be all
coplanar, and they must be distributed over the image space. Since
there are 16 independent parameters in the camera model and each point
contains two dimensions of information in the image plane, at least 8
points are needed, or 6 if the a priori standard deviations are small
enough to add appreciable information. However, it is highly
desirable to have considerably more points than this minimum in order
to obtain an accurate solution for all of the parameters.
4.2 Initialization
In order to obtain initial values for iterating, first a point close
to the camera axis is found by selecting
pa to be the
pi for which x and
y are closest to sh/2 and
sv/2, respectively. Then this and the given data
are used to compute the initial approximations to the camera model
vectors, as follows:
where u is a vector pointing upwards in object space,
and where it is assumed that the image x axis points to the
right and the image y axis points down (from the upper left
corner of the image). (If the y axis points up in the image,
the sign of v0 should be reversed.) The
initial values for  0,
0,  1, and
1, and  2 are zero.
2 are zero.
The a priori weight matrix is computed as follows:
where the fact that the off-diagonal terms for a and
o are negative of the main-diagonal terms causes the
standard deviation  d to
apply to the difference of a and o.
Additional weight can be applied to any other of the initial
approximation values, by adding the reciprocal of the variance to the
appropriate main diagonal element of No).
For example, the position of the camera may be known sufficiently well
to enter this information into the solution by adding appropriate
weight in the first three diagonal elements of
No.
d to
apply to the difference of a and o.
Additional weight can be applied to any other of the initial
approximation values, by adding the reciprocal of the variance to the
appropriate main diagonal element of No).
For example, the position of the camera may be known sufficiently well
to enter this information into the solution by adding appropriate
weight in the first three diagonal elements of
No.
4.3 Iterative Solution
The method described here does a rigorous least-squares adjustment [MIKHAIL1976] in which the camera model
parameters are adjusted to minimize the sum of the squares of the
residuals (differences between measured and adjusted positions of
points) in the image plane. Since the problem is nonlinear, this
requires an iterative solution. However, the method converges rapidly
unless far from the correct solution, and a reasonably good
approximation to start the iterations was obtained in Section 4.2.
The program has an inner loop for iterating the nonlinear solution and
an outer loop for editing (removing erroneous points) by a previously
developed general method [GENNERY1980, GENNERY1986]. The steps in these
computations for the problem here are as follows.
- (This is the beginning of the edit loop.) Set
c, a, h,
v, and o to their initial
approximations (c0,
a0, h0,
v0, and o0),
set
 0,
0,  1, and
1, and  2 to zero, and set the estimated
measurement variance
2 to zero, and set the estimated
measurement variance  2 to 1,
as an initial approximation.
2 to 1,
as an initial approximation.
- (This is the beginning of the iteration loop.) First, the
2-by-18 matrix of partial derivatives of the constraints
(unit(a) = 1 and unit(o) = 1)
relative to g (the parameters) is
For each point i currently retained, compute 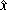 i,
i,  i, and the preliminary
quantities by the equations in Section 2.2; and compute the partial
derivatives of p'i,
i, and the preliminary
quantities by the equations in Section 2.2; and compute the partial
derivatives of p'i, 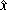 i, and
i, and  i as in Section 3. Then
the 2-by-18 matrix of partial derivatives of
i as in Section 3. Then
the 2-by-18 matrix of partial derivatives of 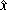 i and
i and  i relative to
g is
i relative to
g is
(since 
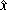 i/
i/ c = -
c = - 
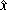 i/
i/ pi, and
similarly for
pi, and
similarly for  i),
and the discrepancies between measured and computed data are
i),
and the discrepancies between measured and computed data are
Compute the matrix of coefficients in the normal equations
N (18-by-18), the "constants" in the normal equations
t (18-by-1), and the sum of the squares of the
discrepancies (which become the residuals when the solution has
converged) q as follows:
where the summations are over all points currently retained,
n is the total number of these points, g
represents the current parameter values, and
go represents the a priori parameter
values (initial approximations). The first term in (31) and (32)
applies the a priori weight to the initial values, and the second term
applies some weight to the constraints. These constraint terms
mathematically have no effect on the solution, since the exact
constraints are applied below in steps 3 and 5. However, they are
necessary to prevent the solution without the constraints from being
singular, and that will be computed first (in step 3, as
(N-1t) before the
constraint equation is applied. The scale factor chosen for these
terms above cause them to have about the same magnitude as the result
of the main summation for N, so that numerical
accuracy is preserved.
- Compute the following (using the exact general constraint
equations provided by Mikhail [MIKHAIL1976]):
Note that a and o are unit vectors
on the first iteration (because of the initial approximations) and on
the last iteration (within the convergence tolerance), but on
intermediate iterations they in general are not. The comparison of
their magnitudes with unity in the above equation is what causes them
to converge to unit vectors. Then add d to the
current values of the camera model parameters to produce the new
values, as follows:
The estimate of measurement variance is
where n is the number of points currently retained (not
rejected), that is, the number of points actually used to obtain
q. The denominator in (37) would be 2n - 16 if
there were no a priori weights. The value 2n - 14 is an
approximation, based on the fact that there usually is a large a
priori weight forcing o to be nearly equal to
a, but not much weight forcing  0,
0,  1, and
1, and  2 to be nearly zero. The exact
value is not very important, since the number of measurements
2n usually is much larger than 14, and usually not much
accuracy is needed or is attainable with variances, anyway.
2 to be nearly zero. The exact
value is not very important, since the number of measurements
2n usually is much larger than 14, and usually not much
accuracy is needed or is attainable with variances, anyway.
- If the magnitude (length of vector) of the change in
c (first three elements of d) is
less than 10-5|pa -
co|, the magnitude of the change in
a (second three elements of d) is
less than 10-5, the magnitude of the change in
h (third three elements of d) is
less than 10-5f/ph, the
magnitude of the change in v (fourth three elements
of d) is less than
10-5f/pv, the magnitude of the
change in o (fifth three elements of
d) is less than 10-5, and the absolute
values of the changes in the
 's (the
last three elements of d) are each less than
10-3, then go to step 5 (exit from the iteration loop).
Otherwise, if too many iterations have occurred (perhaps 20), give up.
Otherwise, go to step 2. (This is the end of the iteration loop.)
's (the
last three elements of d) are each less than
10-3, then go to step 5 (exit from the iteration loop).
Otherwise, if too many iterations have occurred (perhaps 20), give up.
Otherwise, go to step 2. (This is the end of the iteration loop.)
- The covariance matrix of the parameters is
| Cgg =
N-1 - N-1KTM-1KN-1 |
(38) |
If this is the first time here, go to step 8.
- For the last point tentatively rejected, recompute
ei and
Ai as in step 2 using the latest
values of the camera model parameters. Then,
where  is the 2-by-2 identity matrix. If
ri > 16, reject this point.
Otherwise, go to step 9 (exit from the edit loop).
is the 2-by-2 identity matrix. If
ri > 16, reject this point.
Otherwise, go to step 9 (exit from the edit loop).
- If too many points have been rejected (perhaps 10) give up.
- For each current point, use the most recent values in the
following:
Tentatively reject the point with the greatest
ri. Then go to step 1. (This is the end
of the edit loop.)
- Reinstate the tentatively rejected point, and back up to the
solution computed using this point. Use the results from this old
solution below, and finish successfully.
If the run is successful, the camera model parameters
g and their covariance matrix
Cgg are the result.
A possible improvement that may be desirable in the case of grossly
nonsquare pixels would be to compute separate q's for each
image dimension by summing the squares of the discrepancies separately
for x and y instead of using (33), and by dividing by n - 7
instead of 2n - 14 in (37) to obtain the two variances. Then
a 2-by-2 weight matrix with the reciprocal of these variances on the
main diagonal would be included in the summations in (31) and (32) in
the usual way [MIKHAIL1976], instead
of factoring the variance out as above.
5 Use of Camera Model
5.1 Projecting from Object Space to Image Space
When a point pi in
three-dimensional space is available and it is desired to compute its
projection into an image, pi and
the camera model computed in Section 4 are used in (3-12) in Section
2.2 to compute 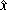 i
and
i
and  i.
i.
Often the partial derivatives of the above projection are needed (for
error propagation or in a least-squares adjustment). These are
obtained as follows:
in terms of the partial derivatives defined in Section 3. However,
for most applications not much accuracy is needed in partial
derivatives. Therefore, when the distortion is small (| 0| << 1, |
0| << 1, | 1| << 1, and |
1| << 1, and | 2| << 1) and speed is
important, sufficient accuracy may be obtained by assuming that
2| << 1) and speed is
important, sufficient accuracy may be obtained by assuming that  p'i/
p'i/ pi is
the identity matrix, so that the following results:
pi is
the identity matrix, so that the following results:
Using these approximations can result in significant savings in time
if many points are to be projected, since the computation of  p'i/
p'i/ pi is
considerably more involved than is the computation of
pi is
considerably more involved than is the computation of 
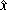 i/
i/ p'i and
p'i and

 i/
i/ p'i, as
can be seen in Section 3.
p'i, as
can be seen in Section 3.
5.2 Projecting from Image Space to Object Space
Sometimes a point in the image (xi and
yi) is given and it is desired to project
it as a ray in space (represented by the unit vector
ri). This can be done by first
projecting the ray neglecting distortion, as follows:
r'i =
sign(a · v ×
h) unit[(v -
yia) ×
(h - xia)] |
(45) |
where "sign" = ± 1 according to whether its argument is
positive or negative. Then the distortion can be added by one of two
methods.
In the first method, (3-7) are used with
pi - c replaced
by ri and
p'i - c replaced
by r'i (which is equivalent to
considering a point at unit distance), to produce the following:
where we have had to rescale ri
to force it to be a unit vector, since otherwise the distortion
correction changes only the component of the vector perpendicular to
the optical axis, and thus changes the length of the vector. However,
the equations in Section 2.2 were designed to go from the unprimed to
the primed quantities, and here the opposite is desired. Therefore,
in this method an iterative solution is done as follows: on the first
iteration, ri is set equal to
r'i; then an improved
ri is computed as above on each
iteration. The values of the other quantities from the last iteration
also are needed below if partial derivatives are computed.
The second method is faster and is one that has been implemented. It
can be derived by manipulating (46-50) to produce the following:
Equation (54) can be solved for µ'i
by Newton's method (using µ'i = 0
as the initial approximation). Then,
However, if partial derivatives are to be computed below, corrected
values of 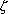 i,
i, 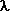 i,
i,  i, and
µi must be computed as in the first
method, by using (46-49(. (Now only one iteration is needed, since
ri has already been obtained.)
i, and
µi must be computed as in the first
method, by using (46-49(. (Now only one iteration is needed, since
ri has already been obtained.)
The partial derivatives of the projection into a ray can be obtained
by differentiating (45) with respect to
xi and yi,
to obtain the following:
Then the effect of distortion can be included by computing the partial
derivatives as in Section 3, with
pi - c replaced
by ri and with a rescaling
because of the change in magnitude due to (50), to produce the
following:
Then, since the transformation in the other direction is desired, the
inverse of the matrix is used, as follows:
As in projecting in the other direction, this correction of the
partial derivatives for distortion can be omitted when speed is
important and not much accuracy is needed, if the distortion is
small.
Acknowledgments
The research described herein was carried out by the Jet Propulsion
Laboratory California Institute of Technology, under contract with the
National Aeronautics and Space Administration. The camera calibration
program was written by Todd Litwin.
 ) will be represented by
|v|, and the unit vector in its direction
(v/|v|) will be represented by
unit(v). The derivative of a vector relative to a
scalar will be considered to be a vector, the derivative of a scalar
relative to a vector will be considered to be a row vector, and the
derivative of a vector relative to a vector will be considered to be a
matrix.
) will be represented by
|v|, and the unit vector in its direction
(v/|v|) will be represented by
unit(v). The derivative of a vector relative to a
scalar will be considered to be a vector, the derivative of a scalar
relative to a vector will be considered to be a row vector, and the
derivative of a vector relative to a vector will be considered to be a
matrix. 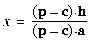
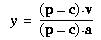


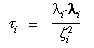
 i is proportional to the
square of this off-axis distance, this polynomial can be written as
follows:
i is proportional to the
square of this off-axis distance, this polynomial can be written as
follows: 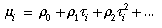
 's are the distortion
coefficients. We use only coefficients up to
's are the distortion
coefficients. We use only coefficients up to 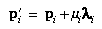
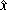 i and
i and
 i) by using
p'i instead of p
in (1, 2). However, for efficiency these equations are expressed in
terms of the intermediate quantities
i) by using
p'i instead of p
in (1, 2). However, for efficiency these equations are expressed in
terms of the intermediate quantities  i,
i, 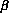 i, and
i, and 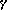 i, as follows, since
these quantities will be needed again in later sections:
i, as follows, since
these quantities will be needed again in later sections: 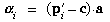
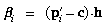

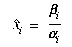
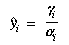
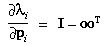

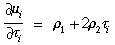
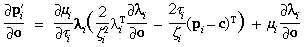
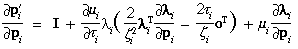
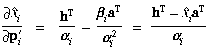
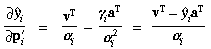
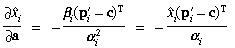
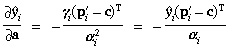
 is the 3-by-3 identity matrix.
The first three of these (derivatives of
is the 3-by-3 identity matrix.
The first three of these (derivatives of 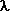 i and
µi) are only intermediate
quantities needed in obtaining the others and will not be used
elsewhere.
i and
µi) are only intermediate
quantities needed in obtaining the others and will not be used
elsewhere.  d (in radians) of the
difference between the optical axis o and the
a vector, the a priori standard deviations about zero
of each distortion coefficient
d (in radians) of the
difference between the optical axis o and the
a vector, the a priori standard deviations about zero
of each distortion coefficient 
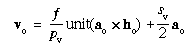

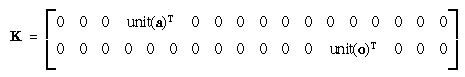
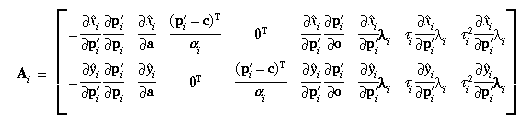

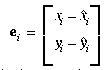
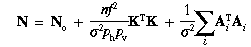


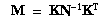
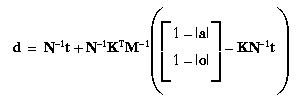
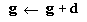
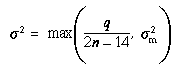
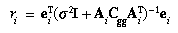
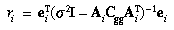
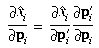
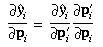
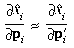


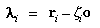
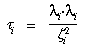

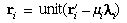
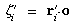
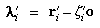

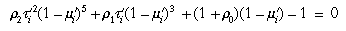
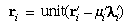
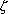 i,
i,